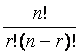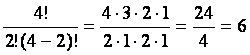|
||
homepage
previous -- view my teaching portfolio here
|
|
Math Notes
Introduction Combinations are similar to permutations except that now order doesnít matter. We are still selecting from a fixed set of elements, such as {5, 6, 7, 8}. The possible combinations we can choose, given no repetitions are: 5678 If we choose fewer than the maximum number of elements, such as two elements would be: 56 57 58 67 68 78 Like permutations, we have a formula
for determining the number of possible combinations of elements without
listing them out, but the formula is slightly more complicated. We can
refer to the formula with the label nCr, C(n, r)
or often just
For instance, in the first example above, we have a
set of four elements, and we are selecting all four elements for our
combination, so our formula gives us
Combinations have a lot of applications in mathematics. We will be seeing some of them below when we discuss the binomial theorem. Another example is Pascalís triangle: Row 0 1 Row 1 1 1 Row 2 1 2 1 Row 3 1 3 3 1 Row 4 1 4 6 4 1 Row 5 1 5 10 10 5 1 Row 6 1 6 15 20 15 6 1 Each row of the triangle is the value of a given n, and the value in the triangle is the value of the combination r+1 entries across the row. For example, in Row 6, the 20, is the 4 element in the row. If 4 = r+1, then r = 3. And if we use the formula given above, 20 is the value of C(6, 3). Worked Examples A. How many dance couples can be formed from a group of eleven people? We are choosing from a set of eleven, and we are choosing two elements, so 11C2 = 11!/[2!(11-2)!] = 11!/(2!9!) = 11*10*9*8*7*6*5*4*3*2*1/(2*1*9*8*7*6*5*4*3*2*1) = 11*10/2 = 55. The combinations formula is the same as P(n, r)/r!. See some of the simpler examples in Counting Methods II. B. Find the value of
5C3 = 5!/[3!(5-3)!] = 5!/(3!2!) = 5*4*3*2*1/(3*2*1*2*1) = 5*4/2 = 10. C. Find the expansion of (a+b)4. We could multiply this out longhand, but according to the binomial theorem, each term of the expansion has the following shape: (nCr)an-rbr. We begin with r = 0 and go up to r = n where n is the degree of the exponent. The first term is (4C0)a4b0 = a4. The second term is (4C1)a4-1b1 = 4a3b. (4C2)a4-2b2 = 6a2b2. (4C3)a4-3b3 = 4ab3. (4C4)a4-4b4 = b4. Now add them all up to get a4 + 4a3b + 6a2b2 + 4ab3 + b4. Problem Solving Tips Some things to look for when solving combination problems:
Additional Problems with Answers 1. How many ways can you be dealt a hand of five cards in poker from a standard deck of playing cards? (Remember that hands don't matter what order you get the cards in.) 2. Find C(8, 6). 3. Find C(8, 2). 4. A company is giving away a trip to Hawaii to its three top sellers. The company has 22 employees. How many possible ways could the vacation trip be given away? 5. One way of winning the lottery is getting all the numbers picked in any order. How many ways can a person pick numbers to cover all the possible combinations of winners if you have to pick six numbers out of 44? 6. In a conference of 9 schools, how many intraconference football games are played during the season if the teams all play each other exactly once? 7. Ms. Mitchell will choose 1 boy and 1 girl from her class to be the class representatives. If there are 4 boys and 7 girls in her class, how many different pairs of class representatives could she pick? Challenge Problems: 8. There are 5 married couples and a group of three is to be formed out of them; how many arrangements are there if a husband and wife may not be in the same group? 9. A door can be opened only with a security code that consists of five buttons: 1, 2, 3, 4, 5. A code consists of pressing any one button, or any two, or any three, or any four, or all five. How many possible codes are there? (Assume all the codes need to be depressed simultaneously.) 10. A person has the following bills: $1, $5, $10, $20, $50. How many unique sums can one form using any number of these bills only once? 11. A three-person committee must be chosen from a group of 7 professors and 10 graduate students. If at least one of the people on the committee must be a professor, how many different groups of people could be chosen for the committee? 12. What are the chances of choosing three balls from a bowl filled with 2 red balls, 3 yellow balls, 4 green balls and 5 blue balls where the three balls you choose consist of exactly 1 green ball and 2 red balls. 13. Write out the expansion of (4x - 3y2)6. 14. What is the 4th term of the expansion of (3x3 - y)8. Answers: 1. 2,598,960 Links to Outside Sources
Permutations and combinations - TheMathPage Links to Supporting Topics Counting Methods I -- With Repetition,
Order Matters: Fundamental Counting Principle History If you know of any links the discuss the history, origin or development of the Fundamental Counting Principle, please email me at the address below. |
| (c) 2005, 2004 by Betsy McCall, all
rights reserved To contact the webmistress, email betsy@pewtergallery.com |
||