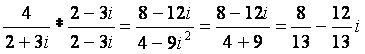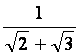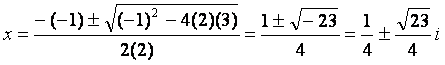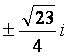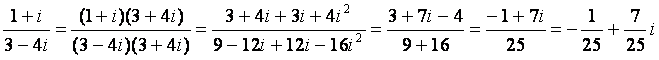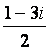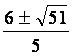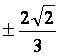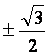 |
||
homepage
previous -- view my teaching portfolio here
|
|
Math Notes
Introduction Complex numbers are the sum of a real number (the kind we're used to
working with) and an imaginary number.
We usually write complex numbers in the form a + bi, where
a and b are both real numbers, and the letter i
indicates which of these elements is the imaginary number
z is the variable we use to refer to complex numbers, rather than x. Complex numbers are made up of a real part and an imaginary part. Re(z) is the notation we use to refer to the real part of a complex number. Im(z) is the notation we use to refer to the imaginary part of a complex number. When a number is written in the form z = a + bi, Re(z) = a, and Im(z) = b. The most common way we encounter complex numbers are through applying
the quadratic formula to quadratic equations which have no real
solution. [To refresh our memories, recall that a quadratic equation is
of the form ax2 + bx + c = 0. The
quadratic formula helps us find the values of x that makes this
equation true.
Consider the example x2
+ x + 1 = 0.
The
complex conjugate, notated by
z, is found by making the
imaginary part of z the opposite sign. So, for instance, if z = a
+ bi, then z = a - bi.
In our example above, one solution is
Complex numbers allow us to make generalizations about polynomials that would not be possible using just real numbers. The most important of these generalizations is the Fundamental Theorem of Algebra, which states that every polynomial of degree n has exactly n roots (counting real, complex and repeated roots). One of the consequences of this theorem, is that every polynomial with real coefficients will have an even number of complex roots. That even number may be zero, or it will be two, four, six, etc. These roots will come in pairs of complex conjugates. We want to be able to perform basic operations on complex numbers as well, such as addition, subtraction, multiplication and division. When we are doing addition
and subtraction, we are going to distribute signs and add like terms
just as we would as if we are using variables. For example: z1
= 3 - 4i and z2 = 2 + 6i, When we are doing
multiplication, at first, we are also going to treat complex numbers as
though we are dealing with a single variable, and FOIL. When we do division, we
have to first remove any imaginary numbers from the denominator.
Consider a number like
This
method of eliminating the imaginary number in the denominator is very
similar to the process we use to rationalize denominators in expressions
like
Sometimes we want to look at complex numbers visually. When we want to look at real numbers, we draw a one-dimensional number line and each point on that line represents a unique real number. But when we want to look at complex numbers, because they have both a real and an imaginary part, we are going to need not one, but two dimensions. This means that complex numbers are graphed not on a line, but on a plane. We can treat complex numbers then like we would any other point in a plane, as a Cartesian coordinate, where the x-coordinate or first coordinate is the real part or Re(z), and the y-coordinate or second coordinate is the imaginary part or Im(z). Now a + bi can be represented as simply (a, b).
The complex plane then looks like the picture at left. The corners of the center square then are, starting in the first quadrant, 1 + i, second quadrant, -1 + i, third quadrant, -1 - i, and fourth quadrant, 1 - i. We will do more with plotting complex numbers in the plane when we move on to Complex Numbers in Polar and Trigonometric Form.
Worked Examples A. State Re(z) and Im(z) for the following complex numbers. a. z = c + di b. z = 3 - 4i c. z = 5 d. z = -4i a. Re(z) = c, Im(z) = d; b. Re(z) = 3, Im(z) = -4; c. Re(z) = 5, Im(z) = 0; d. Re(z) = 0, Im(z) = -4 We report Re(z) to be the part of a complex number lacking an i; we report Im(z) to be the part of the complex number which is attached to the i, but Im(z) is just the coefficient in front of the i, not the i itself. Also note the either the real or imaginary part may be 0. B. Give the real and imaginary parts of the solutions to the quadratic equation 2x2 - x + 3 = 0. Use the quadratic formula to get
C. Give the complex conjugate of a. z = 4 - 6i, b. z = 5, c. z = i To find the complex conjugate, just change the sign of the imaginary part. For a. z = 4 + 6i; for b. z = 5 because there is no imaginary part, it's just like 5 + 0i, and 5 - 0i is exactly the same thing; for c. z = -i. D. For the equation x4 + 3x3 + 6x2 + x - 4 = 0, how many roots does this polynomial have? Since the highest degree term is x4, this is a degree-4 polynomial, so it has to have 4 roots. E. Add and subtract the following complex numbers: z1 = 2 + 4i, z2 = -7 + 3i. When we add we get 2 + 4i
+ (-7 + 3i) = (2 - 7) + (4 + 3)i = -5 + 7i. F. Multiply and divide the following complex numbers: z1 = 1 + i, z2 = 3 - 4i z1*z2
= (1 + i)(3 - 4i) = 3 - 4i + 3i - 4i2 = 3 - i - 4i2
= 3 - i - 4(-1) = 3 - i + 4 = 7 - i. Problem Solving Tips When dealing with complex numbers, there are some strategies you can use:
Additional Problems with Answers 1. State Re(z) and Im(z) of the following complex numbers: a. 4 + 6i
b.
2. Find the real and imaginary parts of the solutions to the following polynomials: a. 5x2 - 12x -3 = 0 b. -3x2 + 2x - 3 = 0 c. x3 - 1 = 0 3. Find the complex conjugates of: a. z = 1 + 0.4i b. z = 3 - 5i c. -.0006i d. i2 4. How many real or complex roots do the following polynomials have? a. x3 - 1 = 0 b. x5 + 6x -2 = 0 c. x6 + 5x4 - 3x2 - x + 4 = 0 5. Given the following complex numbers: z1 = 2 - i, z2 = 3 + 2i, z3 = 4 - 5i, z4 = 2 + 4i, z5 = -2 - 3i, simplify the following expressions: a. z1 + z2 b. z2 + z3 c. z3 - z4 d. z4 - z5 e. z5*z1 f. z1*z3 g. z2/z4 h. z3/z5 6. Plot the following complex numbers in the plane: a. 2 - i b. i c. 1 + 3i d. 4 e. 0 Answers: 1. a.
Re(z) = 4, Im(z)=6; b. Re(z) = 1/2, Im(z) = -3/2; Re(z) = 0, Im(z) = -1;
Re(z) = 1/4, Im(z) = 0 Links to Outside Sources An introduction
to complex numbers Links to Supporting Topics Imaginary Numbers History
Question Corner -- The Origin of Complex Numbers |
| (c) 2005, 2004 by Betsy McCall, all
rights reserved To contact the webmistress, email betsy@pewtergallery.com |
||
.
Let's take a moment to introduce some terms and notation we are going to
use in referring to complex numbers.
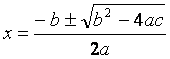Remember that in our formula, the a, b, c refer back to the coefficients
in our original quadratic equation.]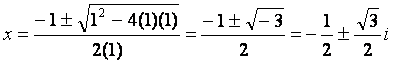
.
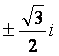
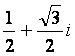
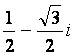
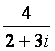In order to remove the imaginary number from the denominator, we are
going to multiply this fraction by 
where z2 is the complex number in the denominator. One
of the things we didn't talk about before when we dealt with complex
conjugates is that when we multiply a complex number by it's conjugate
the result is a purely real number. It's just like multiplying the
difference of squares formula, the middle terms drop out because they
are of different signs. So for this example
