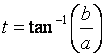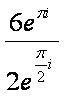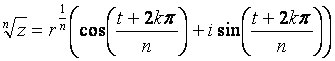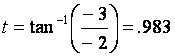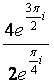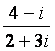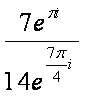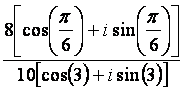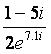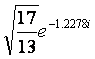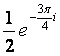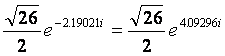|
||
homepage
previous -- view my teaching portfolio here
|
|
Math Notes
Introduction In addition to representing complex numbers in Cartesian form as a + bi, we can also represent complex numbers in polar or trigonometric form. The form gets its name because the form depends on polar coordinates containing an angle, the distance in radians from the positive x-axis, and a radius, the distance from the origin to the point in the plane. It is sometimes called trigonometric form because the form of the complex number contains a cosine and a sine. These forms of complex numbers are equivalent, but they serve different purposes. We will come to what these are later on. If we begin with a complex number in Cartesian form, we can determine it's polar form by calculating r and t, where r is the radius and t is the angle. To find r for a complex number we, need to find the distance
from the origin. We can use the distance formula, and we get the
value of
Then we need to find the
angle t. To do this, we can think of the complex number
forming a right triangle with the x-axis. From trigonometry, we
can use the inverse tangent function to find the angle, given by
To get the polar form, we now use the same transformation that we would for any parametric representation of the x-y plane. We set x = rcos(t) and y = rsin(t). But remember, the x-coordinate here is the real part, and the y-coordinate here is the imaginary part, so a + bi becomes rcos(t) + risin(t). Check our answer. 5cos(.93) = 2.99 and 5sin(.93) = 4.01. This difference here is just a rounding error. These forms of complex numbers also arise from another source, that is in exponential form. Exponential form and polar form are closely related through the formula r*eit = r[cos(t) + isin(t)]. (This equation is referred to as the Euler equation.) This exponential form of complex numbers arise frequently in differential equations. The properties of trigonometric forms of complex numbers can be proved using the exponential form as a starting point and applying well-known properties of exponents. It is through this Euler relationship that we know that the r and the t in both forms are the same, so the same calculations can be used to determine either form. The exponential form of 3 + 4i, using our earlier results is 3 + 4i = 5e.93i. The special properties of the polar form are derived from the properties of the exponential form. For instance, what happens when we multiply two complex numbers in exponential form together? Like (2e.4i)(3e.6i). We are going to multiply the coefficients and add the exponents (since the base is the same in both terms), giving us 6ei. That was a lot easier than working with these numbers in Cartesian form. Compare: 2e.4i = 2cos(.4) + 2isin(.4) = 1.84 + .779i, and 3e.6i = 3cos(.6) + 3isin(.6) = 2.48 + 1.69i; now multiply (1.84 + .779i)*(2.48 + 1.69i) by FOILing. I think you see my point, but let's continue and compare answers. 4.56 + 3.11i + 1.93i + 1.32i2 = 3.24 + 5.04i. What's 6ei? 6cos(1) + 6isin(1) = 3.24 + 5.05i. The difference here is just a rounding error we could easily get rid of by carrying an extra digit. Since exponential and polar form are the same, we can also represent this calculation in the following way. z1*z2 = r1*r2[cos(t1+t2) + isin(t1+t2)]. Just as with the exponential form, we are adding the angles (the exponent portion of the exponential form) and multiplying by the length or coefficient of the exponential form. Just as we saw in the example above, the result is another calculation in polar or trigonometric form. We can carry on this generalization for any number of complex numbers we wish to multiply.
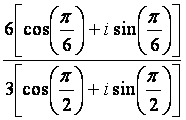
Division is similarly much easier than in Cartesian form. Consider
There's no need to find the complex conjugate to solve this problem. And what did we do? Again, we can represent
this process in polar
form as z1/z2 = (r1/r2)[cos(t1
- t2) the angles, and divided the coefficients. [Note: 6cos(π) + 6isin(π) = 6(-1) + i(0) = -6; and 2cos(π/2) + 2isin(π/2) = 0 + 2i(1) = 2i.] One of the most powerful properties of the exponential and polar forms has to do with raising complex numbers to powers or taking roots of complex numbers. Consider a simple exponential, like et. If we wish to raise this to a large power, like (et)6, we multiply the exponent by the new power, giving us e6t. This is the same process we use to determine large powers of complex numbers. Consider the complex number 1 + i. If we wanted to find (1 + i)6, we have two ways to approach this. We can multiply it out in some way (either by hand or by applying the binomial theorem), or we can convert it into an exponential form (or polar form as we'll see later) and raise that to the sixth power. Let's try it both ways.
Using the binomial theorem: OR
We can do this directly in polar form through the following equation zn = rn[cos(nt) + isin(nt)]. In words, raise the length of the complex number to the desired power, and multiply the angle by the desired power. We can do roots very similarly, but where we multiply in exponential form for multiplication, we will now divide instead (since roots can be represented as fractional exponents, square root is a 1/2 exponent, cube root is a 1/3 exponent and so forth). The rooting process is most useful for determining the roots of unity, or the roots of 1. Consider the equation x5 = 1. What are the values of x that make this work? Well, we know one of them straight off the bat, 15 = 1, but this equation is equivalent to the expression x5 - 1 = 0. We said before that because this is a fifth degree equation, there HAS to be five answers, five total values that, when we multiply the number by itself five times, we get a value of 1 at the end. So far, we've found only one of these values, what are the other four? To introduce our process, let's first start out by checking out our first value using exponential/polar form. How can we write 1 + 0i as a complex exponential? What is our length? Well, clearly, it's 1. What about our angle, well, it turns out to be 0, since our complex number is on the positive x-axis, and tan-1(0) = 0. So, 1 = 1e0i. To take the root of this number, the fifth root in this case, we are going to raise this number to the 1/5 power. (1e0i)1/5 = 11/5*e0i/5 = 1e0i = 1. We get back to where we started, at 1, because 1 to any power is 1, and 0/5 is still 0. The thing about angles, though, is that eventually you come around full circle if your angle is big enough. Big enough, in radians, is 2π. It's still true if you add another 2π to get 4π, and another 2π to get 6π and so on. In angular terms 0 = 2π = 4π = 6π = 8π. But it's exactly these angles that are going to get us our other four roots. Redo the calculation above, but replace 0i with 2πi. (1e2πi)1/5 = 11/5*e2πi/5 = 1e2πi/5 = cos(2π/5) + isin(2π/5) = .3090 + .9511i. (If you can run your calculator in complex number mode, you can check it out, raise this number to the fifth power and you get 1, especially if you carry several digits.) We can repeat this process for the other angles. (1e4πi)1/5 = 11/5*e4πi/5 = 1e4πi/5 = cos(4π/5) + isin(4π/5) = -.8090 + .5878i. (1e6πi)1/5 = 11/5*e6πi/5 = 1e6πi/5 = cos(6π/5) + isin(6π/5) = -.8090 - .5878i. (1e8πi)1/5 = 11/5*e8πi/5 = 1e8πi/5 = cos(8π/5) + isin(8π/5) = .3090 - .9511i. Those are my five roots, and notice that they come in complex conjugate pairs, just as we would have expected. We could continue like this, but if we do, we will just start to repeat the numbers we already have. To describe this procedure directly in polar form
we might write
again we are taking just the primary root of the length of the complex number, and we are dividing the angle by number of the root. The 2kπ term refers to the process of adding multiples of 2π and repeating the process until it either starts to repeat, or we achieve the desired number of roots. It should be noted that polar and exponential forms are less useful for adding and subtracting complex numbers. Convert to Cartesian form to perform these operations, and then convert back if need be. Worked Examples A. Find the polar form and exponential form of the following complex numbers: a. 1 + i b. -i c. 3 d. -2 - 3i For a, we find |z| =
B. Multiply. a. (2e.54i)(3.4e-.89i) b. 4[cos(.12) + isin(.12)]*3[cos(-.7) + isin(-.7)] Multiply the coefficients and add the angles/exponents. For a, 2*3.4 = 6.8 and .54 + -.89 = -.35; thus (2e.54i)(3.4e-.89i) = 6.8e-.35i. For b, 4*3 = 12 and .12 + -.7 = -.58; thus 4[cos(.12) + isin(.12)]*3[cos(-.7) + isin(-.7)] = 12[cos(-.58) + isin(-.58)].
C. Divide. a.
Divide
the coefficients, and subtract the angles/exponents. For a, 4/2 =
2, 3π/2 - π/4 = 5π/4; thus
D. Simplify. (2 - i)5. State your answer in Cartesian form. First convert 2 - i either
to polar or exponential form. |z| =
E.
Simplify.
First
we need to covert 2 - i to exponential or polar form. We did this
in the previous worked example. 2 - i =
Problem Solving Tips
Additional Problems with Answers 1. Find the polar form of the following complex numbers; state the modulus and the argument: a. 1 - i b. -2 c. -3 + i d. 4 + 6i 2. Multiply the following complex numbers as directed, report your answers in polar form: a. (1 + i)(2 - i) b. (3e-4i)(6e3i) c. 2[cos(.4) + isin(.4)]*0.1[cos(2.3) + isin(2.3)] d. (3 - i)(2e.01i) 3. Divide the following complex numbers as directed, report your answers in exponential form: a.
4. Simplify. State your answer in Cartesian form. a. (3 + 3i)7 b. (1 - 2i)4 c. (5 + 3i)8 5. Simplify.
a.
6. Find the following roots of unity:
Answers: 1. a.
|z| = Links to Outside Sources
Lesson on Complex Numbers or Imaginary Numbers Links to Supporting Topics Imaginary Numbers History
Question Corner -- The Origin of Complex Numbers |
| (c) 2005, 2004 by Betsy McCall, all
rights reserved To contact the webmistress, email betsy@pewtergallery.com |
||